XY is a line parallel to side BC of a ∆ ABC. If BE || AC and CF || AB meet XY at E and F, respectively. Show that
ar (∆ ABE) = ar (∆ ACF).
Given XY is a line parallel to BC of a ∆ ABC.
If BE || AC and CF || AB meet XY at E and F, respectively
To prove ar(∆ABE) = ar (∆ACF)
Proof Since, a∆ABC in which XY || BC,
also BE || AC, i.e. BE|| CY and CF || AB, i.e. CF || XB
Now, since EY || BC and CY || BE
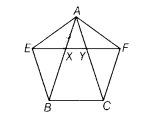
So, EYCB is a parallelogram.
Since, ∆ABE and parallelogram EYCB lie on the same base BE and between the same parallel lines BE and CA.
∴ ar (∆ABE) = 1/2 ar (EYCB) …(i)
Again, CF||BX and XF||BC
∴ BCFX is a parallelogram.
Since, ∆ACF and parallelogram BCFX lie on the same base CF and between the same parallel lines BX and FC.
∴ar (∆ACF) = 1/2 ar (BCFX) … (ii)
Now, parallelogram BCFX and parallelogram EYCB lie on the same base BC and between the same parallel lines BC and EF.
∴ ar (BCFX) = ar (EYCB) …(iii)
From Eqs. (i), (ii) and (iii), we get
ar (∆ACF) = ar(∆ABE)