why is the electric field inside a hollow sphere is zero? even though we consider Gaussian surface where Q=0 won`t the charge on the surface of hollow sphere cause electric field inside hollow sphere? why??
Here, there is an explanation for the electric filed outside the hollow conducting sphere and inside the hollow sphere for your better understanding.
Let us first understand
For electric filed at point outside the conducting sphere.
Outside the conducting surface:
Draw the Gaussian surface outside the conducting surface.
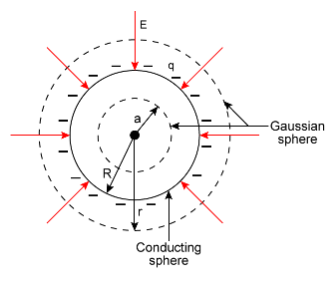
The radius of the Guassian surface drawn outside the conducting sphere is ‘r’
and that for conducting sphere is R. Hence r>R
Let the charge enclosed by this Gaussian surface be q
So the total electric field over the Gaussian surface (r>R) is,
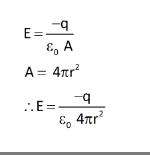
So, this the electric filed outside the conducting sphere.
Inside the conducting surface:
Now, similarly, we will draw the Gaussian surface inside the conducting surface.
In the given figure, you can see the Guassain surface inside the conducting sphere of radius ‘a’
This Gaussian surface encloses no charge.
So using Gauss theorem,
E=0
So as all the charges lies on the surface of conducting sphere, using symmetry and Gauss law the electric field is zero inside the hollow conducting sphere.
So, we can say that the electric field inside any hollow conducting surface is zero provided that there are no charges enclosed by that region.