Using RHS congruence rule, prove that ∆ABC is an isosceles triangle

CBSE Class 9 CBSE Class 9 Maths
1

BE and CF are two equal altitudes of a ∆ABC. Using RHS congruence rule, prove that ∆ABC is an isosceles triangle.
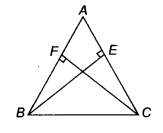
image

2

Given In ∆ ABC, BE = CF and ∠BFC =∠CEB = 90°
To prove ∆ ABC is an isosceles triangle.
image
Proof In ∆BEC and ∆CFB
BE =CF
∠ BEC = ∠ CFB
and BC = BC
image
⇒ ∠ ECB =∠ FBC '[byCPCT]
or ∠ ACB =∠ ABC
⇒ AB = AC
∆ ABC is an isosceles triangle.