Using Gauss law find out electric field intensity due to a line charge.
A line charge is in the form of a thin charged rod with linear charge density λ. Let us find out an expression for electric intensity at any point P at a perpendicular distance r from the rod.
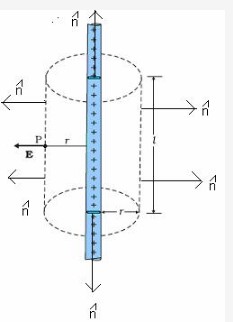
Let us consider a right circular closed cylinder of radius r and length l, with infinitely long line of charge as its axis.
The magnitude of electric field intensity ![]()
at every point on the curved surface of the cylinder is same, because all such points are at the same distance from the line charge.
![]() Contribution of curved surface of cylinder towards electric flux,
Contribution of curved surface of cylinder towards electric flux,
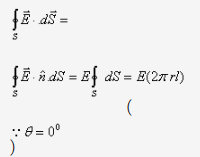
Where ![]() is the curved surface area of cylinder.
is the curved surface area of cylinder.
On the ends of the cylinder angle between ![]()
and ![]() is 90
is 90
. Therefore these ends make no contribution to the electric flux of the cylinder.
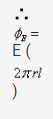
Charge enclosed in the cylinder= linear charge density x length = λl
According to Gauss’s theorem
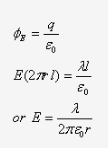
The direction of electric field vector will be the function of whether the line charge is positive or negative
If λ < 0, i.e., in a negatively charged wire, the direction of ![]()
is radially inward towards the wire.
If λ > 0, i.e., in a positively charged wire, the direction of ![]()
is radially out of the wire.