(i) Using Ampere’s circuital law, derive the expression for the magnetic field in the vector from at a point on the axis of a circular current loop.
(ii) What does a toroid consist of ? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open - space interior and exterior to the toroid is zero.
(i) Figure shows, the longitudinal sectional view of long current carrying solenoid.
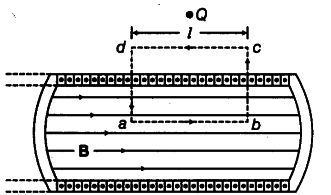
The current comes out of the plane of paper at points marked. B is the magnetic field at any point inside the solenoid.Considering the rectangular closed path abcd. Applying Ampere’s circuital law over loop abcd,
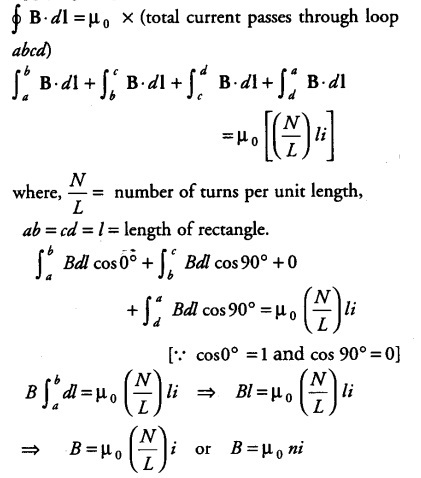
\LJ
where, n = number of turns per unit length.
This is required expression for magnetic field inside the long current carrying solenoid.
(ii) A solenoid bent into the form of closed loop is called toroid. The magnetic field B has a constant magnitude everywhere inside the toroid.
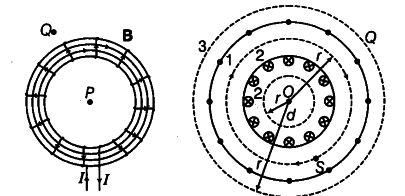
(a) Let magnetic field inside the toroid be B along the considered loop 1 as shown in the figure.
Applying Ampere’s circuital law,
![]()
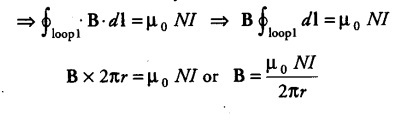
(b) Magnetic field inside the open space interior of the toroid Let the loop 2 be shown in the figure, experience magnetic field B.
No current threads the loop 2 which lie in the open space inside the toroid.
By Ampere’s circuital law,
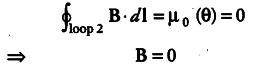
Magnetic field in the open space exterior of the toroid Let us consider a coplanar loop 3 in the open space of exterior of toroid. Here, each turn of toroid threads the loop two times in opposite directions.
Therefore, net current threading the loop = NI-NI = 0
By Ampere’s circuital law,
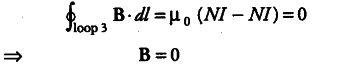
Thus, there is no magnetic field in the open space interior and exterior of the toroid.