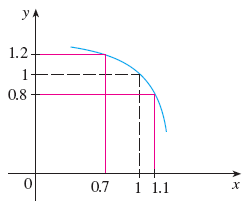
Use the given graph of f to find a number δ such that if |x − 1| < δ then |f(x) − 1| < 0.2
δ= ???
Answer:
Given : | x-1| < ![]()
then |f(x) − 1| < 0.2
To find the number \delta then is to find how close x has to be to 1.
In order for f(x) < 0.2 that is close to 1.
or,
How close does x have to be to 1 (on either side), for f(x) to be between 0.8 and 1.2 ?
So, by the graph :
It is to clear that on the left side of x = 1, x can be within 0.3, but on the right side, it’d have to be within 0.1, of 1, for f(x) to be that close to 1.
Now,
f(x) is within 0.2 of 1 ( which is what | f(x) - 1 | < 0.2 is saying),
we take 0.1, which is sure to work on both sides.
![]()
Here used absolute values around each difference to show that the difference would work on both sides: a positive or negative difference would come out the same.
when we take the absolute values, Looks like it’s leading up to understanding “derivatives” or instantaneous slopes.