Use a table of Laplace transforms to find the Inverse Laplace transform of
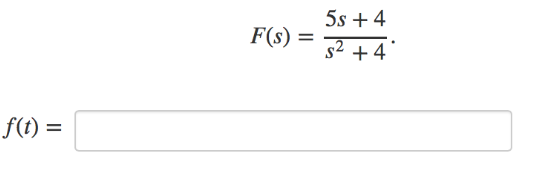
Answer:

From table of Laplace Transform
\pounds^{-1}\left ( \frac{s}{s^2+a^2} \right )=cos(at) \ and \ \pounds^{-1}\left( \frac{a}{s^2+a^2} \right )=sin(at)
Therefore,
f(t)=5\pounds^{-1}\left ( \frac{s}{s^2+2^2} \right )+2\pounds^{-1}\left ( \frac{2}{s^2+2^2} \right )
f(t)=5cos(2t)+2sin(2t)