Two years later, a father will be 8 yr more than three times the age of his son. Taking the present ages of father and son as x and y respectively, write a linear equation for the above and draw its graph. From the graph, find the age of the father, when the son’s age is 10 yr.
Let the present ages of father and son be x yr and y yr, respectively.
Two years later,
Age of father = (x + 2) yr and age of son = (y + 2) yr
According to the question,
Age of father after two years
= 3 (Age of son after two years) + 8
x + 2 = 3(y + 2)+8 =x + 2 = 3y+6+8
x - 3y -12 = 0
which is the required linear equation in two variables.
To draw the graph, we need atleast two solutions of the above equation.
Now, the above equation can be written as
x = 3y +12 ,…(i)
When y = 4,then x = 3x4+12 = 12 +12 =24
When y = 8,then x = 3x8+12 =24+12 = 36
Thus, we have the following table
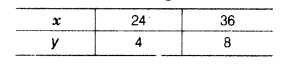
Here, we get the points 4(24, 4) and 6(36, 8). Now, plot the points on the graph paper and join them to get a line AB, which represents the required graph.
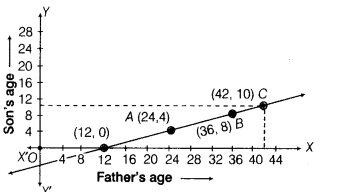
Now, taking point y=10 on Y axis, draw a line parallel to X-axis, which meets the line at point C and from point C, draw a perpendicular, which intersects X-axis at 42 units distance from Y-axis.
Thus, we get point C(42,10), i.e. when son’s age is 10 yr, then the age of father is 42 yr.