Two identical masses, one at rest and the other moving, undergo elastic

[Dhanalakshmi]

Two identical masses, one at rest and the other moving, undergo elastic oblique collision. Prove that they will move at right angles to each other after collision?

[Dhanalakshmi]

Let the equal masses be m and their initial velocities be u and zero respectively.

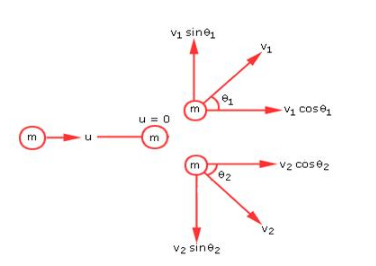
Since momentum is a vector, according to conservation of momentum we have
mu = mv₁cosθ₁ + mv₂cosθ₂
i.e., u = v₁cosθ₁ + v₂cosθ₂ (i)
and 0 = v₁sinθ₁ - v₂sinθ₂ (ii)
Being an elastic collision, kinetic energy is also conserved.


Squaring and adding (i) and (ii), we get


Using (iii) in the above equation, we have


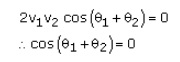
i.e., the masses move at right angles after the collision.