To understand the meaning of capacitance and ways of calculating capacitance

Home Work Help
1

Learning Goal:

To understand the meaning of capacitance and ways of calculating capacitance.

When a positive charge q is placed on a conductor that is insulated from ground, an electric field emanates from the conductor to ground, and the conductor will have a nonzero potential V relative to ground. If more charge is placed on the conductor, this voltage will increase proportionately. The ratio of charge to voltage is called the capacitance C of this conductor: C=q/V.

Capacitance is one of the central concepts in electrostatics, and specially constructed devices called capacitors are essential elements of electronic circuits. In a capacitor, a second conducting surface is placed near the first (they are often called electrodes), and the relevant voltage is the voltage between these two electrodes.

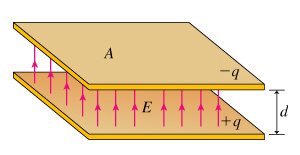
This tutorial is designed to help you understand capacitance by assisting you in calculating the capacitance of a parallel-plate capacitor, which consists of two plates each of area A separated by a small distanced with air or vacuum in between. In figuring out the capacitance of this configuration of conductors, it is important to keep in mind that the voltage difference is the line integral of the electric field between the plates.
image

Part A

  1. What property of objects is best measured by their capacitance?
  2. What property of objects is best measured by their capacitance?

image

Part B

  1. Assume that charge ?q is placed on the top plate, and +q is placed on the bottom plate. What is the magnitude of the electric field E between the plates?
  2. Express E in terms of q and other quantities given in the introduction, in addition to ?0 and any other constants needed.

You did not open hints for this part.
image

Part C

  1. What is the voltage V between the plates of the capacitor?
  2. Express V in terms of the quantities given in the introduction and any required physical constants.

You did not open hints for this part.
image

Part D

  1. Now find the capacitance C of the parallel-plate capacitor.
  2. Express C in terms of quantities given in the introduction and constants like ?0.

image

Part E

Consider an air-filled charged capacitor. How can its capacitance be increased?
You did not open hints for this part.

Consider an air-filled charged capacitor. How can its capacitance be increased?
image

Part F

Consider a charged parallel-plate capacitor. Which combination of changes would quadruple its capacitance?
image

Concepts and reason
The concepts used are capacitance of the capacitor, Gauss law in electrostatics, electric potential, and the capacitance of the parallel plate capacitor.
The property of an object measured by the capacitance is determined by knowing the capacitance of a capacitor.
The electric field between the plates can be calculated by using the electric field due to plane sheet.
By using the relation between the electric field and the potential difference between the plates of the capacitor we can determine the potential difference between the plates of the capacitor.
The capacitance of the parallel plate capacitor is used to calculate the capacitance of the parallel plate capacitor and to know the variation of the capacitance with different physical quantities.

Fundamentals
The capacitance of the capacitor is the ability of a system to store an electric charge and it is the ratio of the change in electric charge in a system to the change in electric potential.
The capacitance of a capacitor is given by,
image

Here, Q is the charge stored in the capacitor and V is the potential difference between the plates of the capacitor.

The electric field defined as the region surrounded all over the charged particle within which another particle experiences the force.
According to Gauss law, the electric field due to plane sheet is given by,
image

Here, is the surface charge density and is the permittivity of free space.

The electrical potential is the amount of work done to bring a positive charge from infinity to the point of reference.
The relation between the electric field and the potential difference between the plates of the capacitor is given by,
V = Ed

Here, V is the potential difference between the plates of the capacitor, E is the electric field, and d is the separation between the plates of the capacitor.
The capacitance of the parallel plate capacitor is given by,
image

Here, is the permittivity of free space, A is the area of each plate, and d is the separation between the two parallel plates.
Use the expression for the capacitance of the capacitor to know the property of an object which can be measured by the capacitance of the capacitor.

Answer:

Part A
The ability to store the charge is the property measured by the capacitance of the capacitor.

Part B
The electric field between the plates is image.

Part C
The potential between the plates is 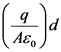image.

Part D
The capacitance of a parallel plate capacitor is image.

Part E
The capacitance of the parallel plate capacitor increases with decrease in the spacing between the plates of the capacitor.

Part F
The capacitance of the parallel plate capacitor quadruples when the separation between the plates reduced to half of its initial separation and doubles the area of the plates.