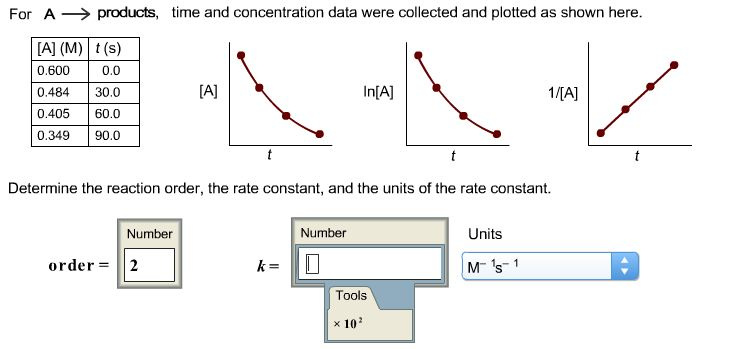
time and concentration data were collected and plotted as shown here.
Concepts and reason
The concepts used to solve this problem are the concept of the reaction rate, order of reaction and rate constant. The reaction rate or rate of a reaction is referred as the rate of disappearance of the reactants in a unit time or rate of appearance of products in a unit time.
The order of a reaction is referred as the exponent or index, to which the concentration term in a rate equation is increased. Rate constant represents a coefficient of proportionality, which relate the reaction rate to the concentration of reactant or product of reactants at any given temperature. The units of the rate constant depends on the order of the reaction.
Fundamentals
The order of a reaction is referred as the exponent or index, to which the concentration term in a rate equation is increased. For single-step reactions, order is equivalent to the stoichiometric coefficients for each reactant. In order to evaluate order of reaction from the set of data comprising concentration value versus time, following 3 graphs are made:

Rate constant represents a coefficient of proportionality, which relate the reaction rate to the concentration of reactant or product of reactants at any given temperature. It is calculated from the value of the concentration of reactants and the order of reaction. The unit of the rate constant depends on the order of the reaction.
For a second order reaction, relation between rate constant and concentration of reaction is as follows:

Answer:
For a reaction,
![]()
The time and concentration data are collected and plotted as follows:

The reaction is a second order reaction. Thus, the order of reaction is 2.
In the above-mentioned problem, the graph given is linear for the 1/[A] verses t. It is characteristic of a second order reaction. This can be explained as follows:
According to the second-order rate law,

As the reaction is a second-order reaction, the rate equation can be written as follows:

The value of the concentration [A] at different time interval is given in this case. By putting the value of concentration at t equals to zero and t equals to 30 s in the above-mentioned formula, the rate constant can be calculated.
The equation of the second order equation will give the value of rate constant. As the reaction is a second-order reaction, the rate equation can be written as follows:
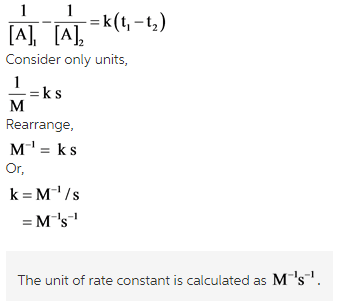
The value of the concentration [A] at different time interval is given in this case. By putting the unit of concentration and unit of time in the above-mentioned formula, the unit of rate constant can be calculated.