The upper half of an inclined plane with an inclination a, is perfectly smooth, while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom, if the coefficient of friction for the lower half is given by:
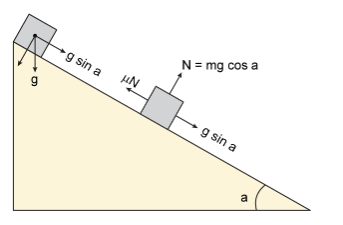
Refer the diagram above. For upper half which is smooth, the acceleration is g×sin(a).
Since the object starts from rest the final velocity when it reaches the end of upper half is √( g×l×sin(a) ).
For the lower part the acceleration is ( g×sin(a) - μ×g×cos(a) ) due to friction
Since the oblect comes to rest when it reaches the bottom of inclined plane
we use the relation " u2 + 2αs = 0 ", where α is acceleration.
Hence ( g×l×sin(a) ) = -2 ( g×sin(a) - μ×g×cos(a) ) (l/2)
Solving for μ we will get μ = 2 × tan(a)