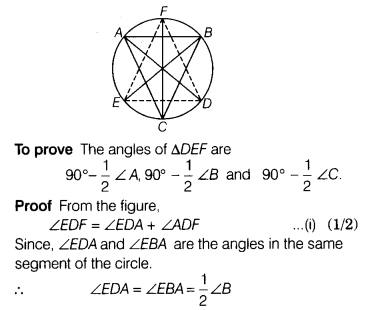
The bisectors of angles A, B and C of a ∆ ABC intersect its circumcircle at D, E and F, respectively. Prove that the angles of the ∆DEF are 90° - 1/2∠A, 90° - 1/2∠B and 90° - 1/2∠C, respectively.
Given AD, BE and CF are the bisectors of ∠A, ∠B and ∠C respectively of ∆ABC and intersect its circumcircle at D, E and F.