Symbol ‘X’ indicates the direction of a magnetic field into the page. A straight long wire carrying current along its length is kept perpendicular to the magnetic field. What is the magnitude of force experienced by the wire ? In what direction does it act ? (Fig. 5)
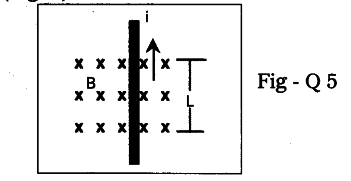
- Let us find the magnetic force on the straight wire carrying current Which is kept perpendicular to the uniform field ‘B’.
- This ‘B’ is directed into the page. It is represented by X’ in figure.
- Let the field confines to the length L. So only the part of the wire of the length ‘L’ is inside the magnetic field. Remaining wire is outside the magnetic field.
- We know that the electric current means charges in motion hence they move with a certain velocity called drift velocity V.
The magnetic force on single charge is given by
$F _{ 0 }$ = qyB .
Let total charge inside the magnetic field be Q. So magnetic force on the current carrying wire is given by
F = QvB —> (1)
The time taken by the charge Q to cross the field is
t=L/v —><(2)
We can write the equation (1) as
F = (Q/t)(vt)B ------>
From (2) vt = L
Substituting this in equation (3) we get
F = (Q/t) LB
But Q/t = I electric current in the wire substituting I in the equation (3) we get
F =. ILB
The direction of force acting on a current carrying wire placed in a magnetic field is perpendicular to the direction of current and perpendicular to the direction of magnetic field.
