suppose we are testing Ho: p=.20 vs Ha: p does not equal .20 and TS= 2.34. What is the p-value?
Concepts and reason
Sampling Distribution of Proportion:
The random sample of size n is taken from the population with proportion P.
The sample proportion has mean P and the standard deviation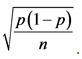
. Moreover, the sample proportion follows normal distribution for large sample size n.
Statistical hypotheses testing: Hypotheses testing is used to make inferences about the population based on the sample data. The hypotheses test consists of null hypothesis and alternative hypothesis.
Fundamentals
The formula for finding the two-sided p-value is 
Answer:
From the information, the test statistics is 2.34. The null and alternative hypotheses are given as:
Null hypothesis:
Alternative hypothesis:
Using the test statistic the p-value is to be calculated.
The null hypothesis states that there is evidence that the population proportion is equal to 0.20. And alternative hypothesis states that there is no evidence that the population proportion is equal to 0.20. The test is two-tailed test and the test statistic is obtained by using the standard normal distribution. The main objective of the problem is to obtain two sided p-value.
The p-value is obtained as shown below:
From the given information, the test statistic is,
and the test is two tailed test.
The p-value is,
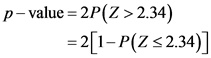
From ’Standard Normal Table’ the area to the left of 
is 0.9904. Hence,
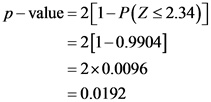
The p-value is 0.0192.
The p-value is obtained by multiplication of the probability of 
with 2. First calculate the probability of 
. It is calculated by taking the value that is intersected with the row containing the value ‘2.30’ and the column containing the value ‘.04’, from the standard normal table.
The p-value is 0.0192.