State Gauss theorem in Electrostatics. Apply Gauss theorem to find electric field strength near an infinite plane sheet of charge.
OR
Briefly explain the principle of a capacitor. Derive an expression for the capacitance of a parallel plate capacitor, whose plates are separated by a dielectric medium.
Gauss"s Theorem: It states that net electric flux diverging normally from a closed surface is equal to 1/ε0 times the net charge enclosed by the surface.
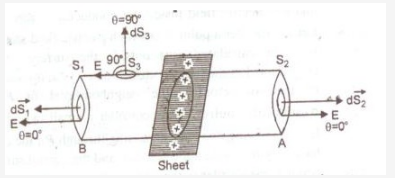
Let electric charge be uniformly distributed over the surface of a thin, non-conducting infinite sheet. Let the surface charge density(i.e., charge per unit surface area) be 
. We have to calculate the electric field strength at any point distant r from the sheet of charge. To calculate the electric field strength near the sheet, we now consider a cylindrical Gaussian surface bounded by two plane faces A and B lying on the opposite sides and parallel to the charged sheet and the cylindrical surface perpendicular to the sheet (fig) By symmetry the electric field strength at every point on the flat surface is the same and its direction is normal outwards at the points on the two plans surface and parallel to the curved surface.
Total electric flux
OR
Principle of a capacitor: A capacitor works on the principle that the capacitance of a conductor increase appreciably when an earthed conductor is brought near it. Thus a capacitor has two plates separated by a distance having equal and opposite charges.
Parallel Plate capacitor: Consider a parallel plate capacitor having two plane metallic plates A and B, placed parallel to each other (fig) The plates carry equal and opposite charges +Q and -Q respectively.
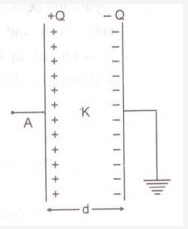
In general, the electric field between the plates due to charges +Q and -Q remains uniform, but at the edges, the electric lines of force deviate outward. If the separation between the plates is much smaller than the size of plates, the electric field strength between the plates may be assumed uniform.
Suppose A be the area of each plate, ‘d" the separation between the plates, K the dielectric constant of medium between the plates. If is the magnitude of charge density of plates, then
This is a general expression for capacitance of parallel plate capacitor. Obviously, the capacitance is directly proportional to the dielectric constant of medium between the plates.
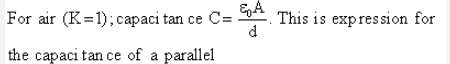
Plate air capacitor. Obviously, the capacitance of parallel plate (air) capacitor is :
a) directly proportional to the area of each plate.
b) inversely proportional to the distance between the plates.
c) independent of metal of plates