state and prove the perpendicular and parallel axis theroem on moment of inertia. the moment of intertia of ring of mass M and radius R about on axis.
Parallel Axis Theorem :- The moment of Inertia of an object about an arbitrary axis equasl the moemnt of inertia of the object about an axis passing through centre of mass and parallel to this arbitrary axis plus the total mass times the squared distance between the two axes.
Mathemeatically, I = Icm + M×h2 ; where I and Icm is the moment of inertia about an arbitrary axis and moment of inertia about centre of mass respectively.
M is the mass of object and h is the distance between the axes.
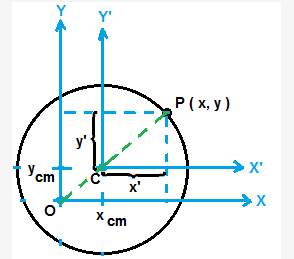
Let us consider a ring of mass M. Let us consider an arbitrary axis passing through a point O about which we need to get moment of inertia of the given ring.
Let us choose our coordinate system that has origin at O. Let us consider a small mass Δm at P that has coordinate (x, y).
Let the coordinate of centre of mass be (xcm, ycm);
Moment of inertia ΔI of the mass Δm about an axis passing through O is given by, ΔI = Δm×(x2+y2)
Total moment of Inertia I = ∑ ΔI = ∑ { Δm×(x2+y2) }
Hence I = Icm+M×h2
Perpendicular-axis theorem:- Moment of Inertia of an object about a given axis is sum of moment of inertia of same object about the two axes which are mutually perpendicular to the given axis.
Let the given axis about which we need Moment of inertia is in Z direction, then Iz = Ix+Iy
where Ix and Iy are moment of inertia about x and y axis respectively.
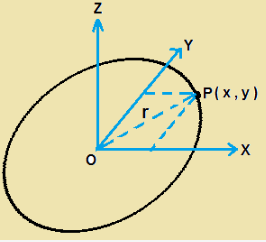
Let us consider a ring of mass M and also consider the coordinate sytem with origin at O as shown in figure. Z-axis of coordinate system is perpendicula to the plane of ring. Let us consider a small mass Δm at P with coordinate (x,y).
Moment of inertia of Δm with respect to x-axis and y-axis are ΔIx +ΔIy = Δm ×(x2+y2) = Δm×r2
But Δm×r2 is the moment of inertia of Δm with respect to z-axis
Hence ∑( ΔIx +ΔIy )= ∑ (Δm ×(x2+y2) )= ∑ (Δm×r2 ) = ∑ ΔIz
hence Iz = Ix+Iy
