State and prove the exterior angle property of a triangle

CBSE Class 7
1

State and prove the exterior angle property of a triangle.

2

** Statement:**
An exterior angle of a triangle is equal to the sum of its interior opposite angles.

Consider triangle ABC.
∠ACD is an exterior angle.
Through C, draw
CE//BA
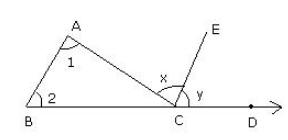
image
To prove:
∠ 1 + ∠2 = ∠ACD
Proof:
∠1 = ∠x (pair of alternate interior angles since, CE||BA)
∠2 = ∠y (pair of corresponding angles)
∠1 + ∠2 =∠x + ∠y
i.e.
∠1 + ∠2 = ∠ACD [∵∠x + ∠y = ∠ACD]
Hence proved.