State ampere’s circuital law and express it mathematically.
Ampere’s law states that the path integral or line integral over a closed loop of the magnetic field produced by a current distribution is given by
![]()
here I refers to the current enclosed by the loop.
Ampere’s law is a useful relation that is analogous to Gauss’s law of electrostatics. It is a relation between the tangential component of magnetic field at points on a closed curve and the net current through the area bounded by the curve.
To evaluate the expression for
![]()
, let us consider a long, straight conductor carrying a current I, passing through the centre of a circle of radius r in a plane perpendicular to the conductor.
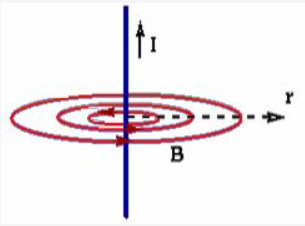
According to Biot-Savart law of magnetism, the field has a magnitude
![]()
at every point on the circle, and it is tangent to the circle at each point.
The line integral of
![]()
around the circle is
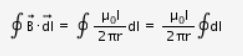
Since
![]()
is the circumference of the circle,
Therefore,
![]()