Show that the quadrilateral formed by joining the mid-points of the sides of a rhombus taken in order, form a rectangle.
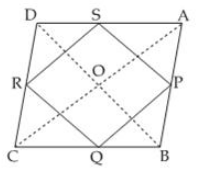
Let ABCD be a rhombus and P, Q, R and S be the mid-points of sides AB, BC, CD and DA respectively.
In ∆ ABD and BDC we have
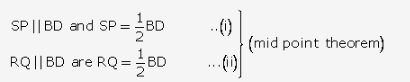
From (i) and (ii) we get
PQRS is a ||gm
As diagonals of a rhombus bisect each other at right angles.
∴ AC ⊥ BD
Since SP||BD, PQ||AC and AC⊥BD
![]()
From above results, we have
||gm PQRS is a rectangle.