Show that the line segment joining the mid-points of a pair of opposite sides of a parallelogram

CBSE Class 9 CBSE Class 9 Maths
1

Show that the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.

2

Let ABCD is a parallelogram. M and N are the
mid-points of AB and DC, respectively.
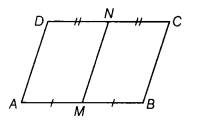
image
To prove ar (parallelogram AMND)=ar (parallelogram MBCN)
Proof Since, ABCD is a parallelogram.
∴ AB = DCan6 AB||DC
[by property of parallelogram]
image
=> AM = DN and AM||DN
[∵ M and N are the mid-points of AB and DC]
So, AMND is a parallelogram.

Similarly, we can prove that MBCN is also a parallelogram.
∴Parallelograms AMND and MBCN are on same base AB and between the same parallel lines AB and DC.
ar (parallelogram AMND) = ar (parallelogram MBCN)