Show that the energy stored in a parallel plate capacitor is 1/2 CV2. Hence derive an expression for the energy density of a capacitor.
When a capacitor is charged by a battery, work is done by the charging battery at the expense of its chemical energy. This work is stored in the capacitor in the form of electrostatic potential energy.
Consider a capacitor of capacitance C. Initial charge on capacitor is zero. Initial potential difference between capacitor plates = zero. Let a charge Q be given to it in small steps. When charge is given to capacitor, the potential difference between its plates increases. Let at any instant when charge on capacitor be q, the potential difference between its plates V=q/C
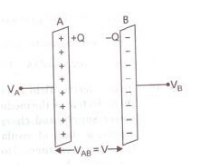
Now work done in giving an additional infinitesimal charge dq to capacitor
dW = V dq = q/C dq
The total work done in giving charge from 0 to Q will be equal to the sum of all such infinitesimal works, which may be obtained by integration. Therefore total work