Show that the area under velocity-time graphs for uniform acceleration gives the distance traveled s = ut + 1/2at2
By Geomtry :-
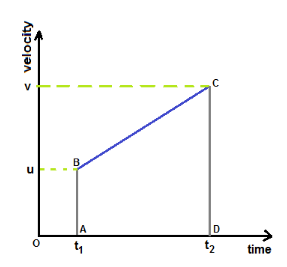
Let a body starts with initial velocity u at time t1, moves with uniform acceleration and its final velocity at time t2 is v.
The velocity-time graph shows the plot for this movement.
The area under the line BC that represents the above movement is a trapezium ABCD.
Area of trapezeium = (1/2)[AB+CD]×(t2-t1)
let (t2-t1) = t , then Area of trapezium = (1/2)[u+v]×t …(1)
if we substitute the definition of acceleration i.e., v = u+at in (1) we get area = u×t +(1/2)a×t2
Since the area under the curve in a velocity-time graph is the distance traveled S, we write the equation as
S = u×t +(1/2)a×t2
By Calculus:
velocity = dS/dt = v(t) …(1)
where S is displacement, v(t) is velocity which is function of t.
hence we write, dS = v(t)dt …(2)
By integrating eqn.(2), we get the total displacement S which is written as
![]()
where u is initial velocity and a is acceleration