The diagonal AC of a parallelogram ABCD bisects ∠A (see the figure). Show that
(i) it bisects ∠C also.
(ii) ABCD is a rhombus.
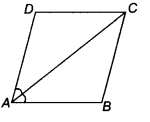
(i) Given, diagonal AC of a parallelogram ABCD
bisects ∠A.
![]()
Here, AB || CD and AC is transversal.
∴ ∠ DCA = ∠ BAC [pair of alternate angle]… (ii)
Similarly, as BC || AD and AC is a transversal.
∴ ∠ BCA = ∠DAC [pair of alternate angle]… (iii)
From Eqs. (i), (ii) and (iii), we get
∠DAC = ∠BCA = ∠BAC = ∠DCA … (iv)
Thus, diagonal AC also bisects ∠C.
(ii) Now, In ∆ ADC, we have
∠DAC =∠DCA [from Eq. (iv)]
=> CD = AD [∵sides opposite to equal angles are equal]
Also, we have AB =CD and AD = BC
[opposite sides of parallelogram]
∴ AB = CD = AD = BC
Hence, ABCD is a rhombus.