(a) Show how Biot-Savart law can be alternatively expressed in the form of Ampere’s circuital law.
Use this law to obtain the expression for the magnetic field inside a solenoid of lengthcross- sectional area ‘A’ having ‘N’ closely wound turns and carrying a steady current ‘I’.
Draw the magnetic field lines of a finite solenoid carrying current I.
(b) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical
wires at its ends. A current of 5.0 A is set up in the rod through the wires.
Find the magnitude and direction of the magnetic field which should be set up in order that the tension in the wire is zero.
Any surface carrying current can be divided into
small line elements, each of length ‘dl’. Considering the tangential components of the magnetic field and finding B . dl sum of all elements tends to the integral, which can be expressed in the following form
![]()
This form is known as Ampere’s circuital law.
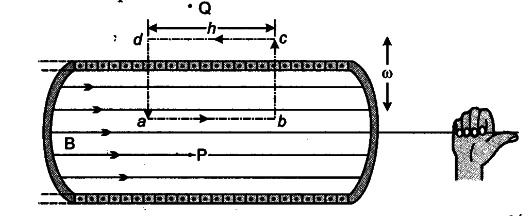
Let ‘n’ be the number of turns per unit length. Then total number of turns in the length ‘h’ is nh.
Hence, total enclosed current = nhI
Using Ampere’s circuital law
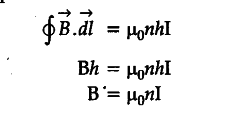
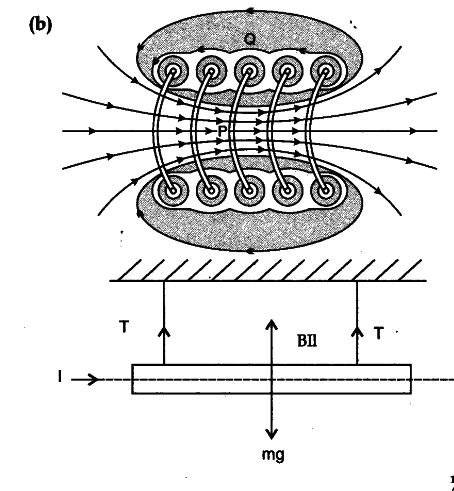
As per the given figure, magnetic field must be vertically inwards, to make tension zero, (If a student shows current in opposite direction the magnetic field should be set up vertically upwards
I/B=mg
For tension to be zero
B = mg/Il = 60 x 9.8 x {{10}^{-3}} / 5.0 x 0.45 T
= 0.26 T