Prove that the sum of the angles in the four exterior segments of a cyclic quadrilateral is equal to 6 right angles.
Let, ABCD be a cyclic quadrilateral and let, angles ∠P,∠Q,∠R and ∠S are in the four external segments.
To prove∠P + ∠Q + ∠R + ∠S = 6 right angles.
Construction Join SB and SC.
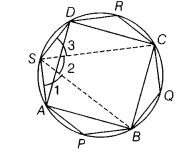
Proof Since, APBS is a cyclic quadrilateral and sum of opposite pairs of angles in a cyclic quadrilateral is 180°.
∴ ∠1 +∠P = 180°
Similarly, BQCS and CRDS are cyclic quadrilaterals.
∴ ∠2+ ∠Q = 180° …(ii)
and ∠3+ ∠R = 180°…(iii)
On adding Eqs. (i), (ii) and (iii), we get
∠1+ ∠P + ∠2+ ∠Q + ∠3+ ∠R = 180° + 180° + 180°.
∠P + ∠Q + ∠R + ( ∠1+ ∠2 + ∠3) = 3x180°
∠P + ∠Q + ∠R+ ∠S =6x90° (1)
[∴ ∠1+ ∠2+ ∠3 = ∠S]
∠P + ∠Q + ∠R+ ∠S =6 right angles