Prove that the sum of any two sides of a triangle is greater than twice the length of the median drawn to the third side.
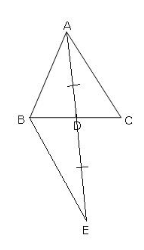
Given: In triangle ABC, AD is the median drawn from A to BC.
To prove: AB + AC > AD
Construction: Produce AD to E so that DE = AD, Join BE.
Proof:
Now in
∆ADC and ∆EDB,
AD = DE (by const)
DC = BD(as D is mid-point)
∠ADC =∠EDB (vertically opp.∠s)
Therefore,
In
∆ABE, ∆ADC![]() ∆EDB(by SAS)
∆EDB(by SAS)
This gives, BE = AC.
AB + BE > AE
AB + AC > 2AD
∵ AD = DE and BE = AC)
Hence the sum of any two sides of a triangle is greater than the median drawn to the third side.