Prove that the lenghts of tangents drawn from an external point to a circle are equal.
Given: A circle with centre O; PA and PB are two tangents to the circle drawn from an external point P.
To prove: PA = PB
Construction: Join OA, OB, and OP.
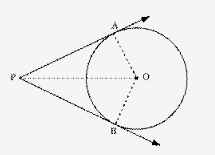
It is known that a tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OA⊥PA and OB⊥PB … (1)
In ∆OPA and ∆OPB:
∠OAP =∠OBP (Using (1))
OA = OB (Radii of the same circle)
OP = OP (Common side)
Therefore,∆OPA
OPB (RHS congruency criterion)
∴ PA = PB
(Corresponding parts of congruent triangles are equal)
Thus, it is proved that the lengths of the two tangents drawn from an external point to a circle are equal.