Consider two molecules A and B. Taking the molecules to be spherical, if r is the radius of the molecules then the distance of closest approach between the two molecules = 2 r (as shown in Figure). This is the distance between the centres of their nuclei.
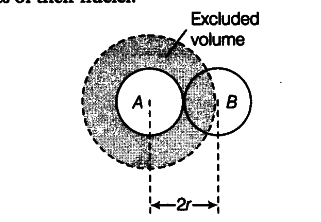
Since the molecules cannot come closer than distance 2r, the excluded volume for a pair of molecules = volume of sphere of radius 2r
= 4/3 \pi ( 2{{r})^{3}} = 8 x 4/3 \pi {{r}^{3}}
Excluded volume per molecule (b) =
1/2 (8 x 4/3 \pi {{r}^{3}})= 4 x 4/3 \pi {{r}^{3}}
But 4/3 \pi {{r}^{3}} = V_{ m }
i.e., the actual volume of the gas molecule.
b= 4 V_{ m }