In the adjoining figure, ABCD is a parallelogram and a line through A cuts DC at P and BC produced at Prove that
ar (∆BPC) = ar (∆DPQ)
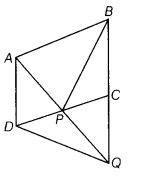
Given ABCD is a parallelogram, so AB || CD and AD || BC. Lines AQ and DC intersect at P.
To prove ar (∆BPC) = ar (∆DPQ)
Construction Join AC.
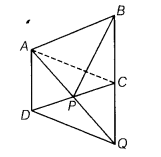
As ∆ADC and ∆ADQ being on the same base AD and between the same parallel lines AD and BQ.
∴ ar (∆ADC) =ar (∆ADQ)
On subtracting ar (∆ADP) from both sides, we get
ar (∆ADC) - ar (∆ADP) = ar (∆ADQ) - ar (∆ADP)
ar (∆APC) = ar (∆DPQ)… (i)
Also, ∆APC and ∆BPC being on the same base PC and between the same parallel lines PC and AB.
So, they are equal in area,
i.e. ar (∆APC) =ar (∆BPC) …(ii)
From Eqs. (i) and (ii), we get
ar(∆BPC) = ar(∆DPQ)