Point C is called a mid-point of line segment AB. Prove that every line segment

CBSE Class 9 CBSE Class 9 Maths
1

Point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.

2

Here, C is the mid-point of line segment AB, such that
AC = BC
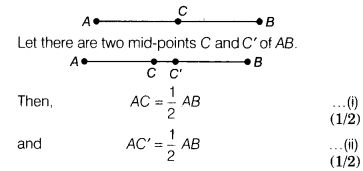
image
From Eqs. (i) and (ii),
which is only possible, when C and C’ coincide.
Therefore, points C and C’ are identical.
Hence, every line segment has one and only one mid-point.