Part A- What is the magnitude of the electric field at the dot in the figure?
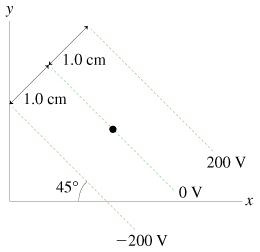
Part A- What is the magnitude of the electric field at the dot in the figure?
Express your answer using two significant figures.
E = _________V/m
Part B -
What is the direction of the electric field at the dot in the figure? Choose best answer.
(a) the negative x-axis.
(b) the positive x-axis.
(c ) 45 below -x-axis
(d) 45 below +x-axis
Concept and reason
The concepts used are electric field and the equipotential lines. By using the relation between the electric field and the potential difference between the plates of the capacitor we can determine the magnitude of the electric field at the dot.
The relation between the equipotential lines and the electric field lines is used to calculate the direction of the electric field vector at the dot.
Fundamentals
The electric field defined as the region surrounded all over the charged particle within which another particle experiences the force.
The relation between the electric field and the potential difference between the plates of the capacitor is given by,
![]()
Here, V is the potential difference between the plates of the capacitor, E is the electric field, and d is the separation between the plates of the capacitor.
The equipotential lines are the contour lines of equal electric potential. The electric field lines and the equipotential lines are mutually perpendicular to each other.
Answer:
Part A
The expression for the strength of the electric field E in terms of the potential difference V and the separation between the plates d is given by,
![]()
Substitute 200 V for V and 1.0 cm for d in above equation as follows:

After rounding off the final answer to two significant figures the strength of the electric field is ![]()
Part B
From the figure it is clear that the equipotential lines are parallel to each other and one of them is passing through the dot.
The following figure shows the direction of the electric field.
The line drawn perpendicular to the equipotential lines and passing through the dot represents the direction of the electric field.
So, a perpendicular line is drawn to the equipotential lines from the dot. Now, used the property of triangle that is total angle is equal to 180 degrees.
From the rule of triangle, if two of the angles are 90 degrees and 45 degrees, then the third angle must be equal to 45 degrees only.
Thus, from the above provided figure, it can be concluded that the angle made by the electric field with x-axis is 45 degrees and it is measured below the negative x-axis.
Part B
The electric field makes an angle of ![]() with the negative x- axis.
with the negative x- axis.