One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the liquid column of mercury in the U-tube executes simple harmonic motion.
The suction pump creates the pressure difference. Hence mercury rises in one limb of the U-tube. When it is removed a net force acts on the liquid column due to the difference in levels of mercury in the two limbs and therefore the liquid column executes S.H.M. which can be explained as follows :
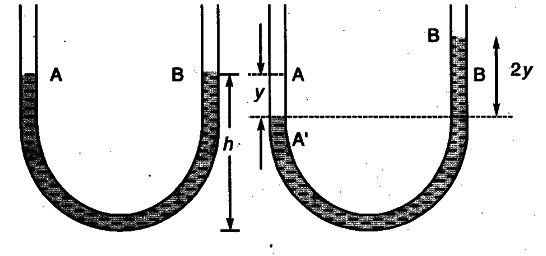
The mercury contained in a vertical U-tube upto the level A and B in its two limbs.
Suppose p = density of the mercury.
L = Total length of the mercury column in both the limbs.
A = internal cross-sectional area of U-tube. Vi m = mass of mercury in U-tube = LAp.
Suppose the mercury be depressed in left limb to A’ by a small distance y, then it rises by the same amount in the right limb to position B’
.•. Difference in levels in the two limbs = A’B’ = 2y.
Volume of mercury contained in the column of length 2y = A x 2y
.-. m = A x 2y x p.
When w = weight of liquid contained in the column of length 2y.
Then w = mg = A x 2y x p x g.
This weight produced the restoring force (F) which tends to bring back the mercury to its equilibrium position.
F = - 2 Aypg = - (2Apg)y
