On the basis of the kinetic theory of gases derive an expression for the pressure exerted by a gas in terms of density and velocity of the molecules.
Consider a cubical vessel (of side l) with walls perfectly elastic as in the figure. Let the vessel have one gram molecule of a gas with its molecules in random motion.
Consider a molecule (mass m) moving with a velocity c, that can be resolved into three components u, v, and w in the direction of the edges of the cube along x, y, z ases.
Therefore, c2 = u2 + v2 + w2 …(i)
Let us consider two faces of the cube, say P and Q, normal to x-axis. When the molecule collides with the side Q with a velocity u, it rebounds with -u, while its other components remain unchanged.
Change in momentum of the molecule due to this collision = -2mu, which is imparted to the wall per collision.
The time taken by molecule to cover distance l = l/u
Therefore, after every interval of time 2l/u, the molecule will again collide with the wall Q, and the number of collisions per unit time with the wall Q is equal to u/2l.
Therefore, Momentum imparted to the wall per unit time = 2mu x u/2l = mu2/l (ignoring the negative sign).
The pressure exerted on the wall Q due to one molecule =![]()
If the vessel contains N molecules with velocities u1, u2, u3…un along x-axis, then the pressure exerted by them on Q, say
![]()
![]()
![]()
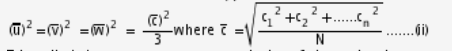
As the molecules moves radomly,
![]()
![]()
This equation give the pressure exerted by the gas on the walls of the vessel it has the same value in any direction the molecule no preference for direction
![]()
