On an open ground, a motorist follows a track that turns to his left by an angle of 60° after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
The distance after which motorist take a turn = 500 m
As motorist takes a turn at an angle of 60° each time, therefore motorist is moving on a regular hexagonal path. Let the motorist starts from point A and reaches at point D at the end of third turn and at initial point A at the end of sixth turn and at point C at the end of eight turn.
Displacement of the motorist at the third turn = AD
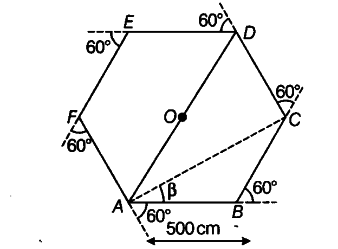
= AO + OD = 500 + 500 = 1000 m
Total path length = AB + BC + CD
= 500+ 500+ 500 = 1500 m
Magnitude of Displacement / Total path length = 1000/1500 = 2/3 = 0.67
At the sixth turn motorist is at the starting point A.
Displacement of the motorist at the sixth turn = 0
Total path length = AB + BC + CD + DE + EF + FA = 500 +500 +500+500+500+500 = 3000m
Magnitude of displacement / Total path length = 0/3000 = 0
At the eight turn, the motorist is point C.
Displacement of the motorist = AC
Using triangle law of vector addition,
Displacement of the motorist at the end of eighth turn is 866 m making an angle 30 degrees with the initial direction of motion.
Total path length = 8 x 500 = 4000m
Magnitude of displacement / total path length = 0.22
