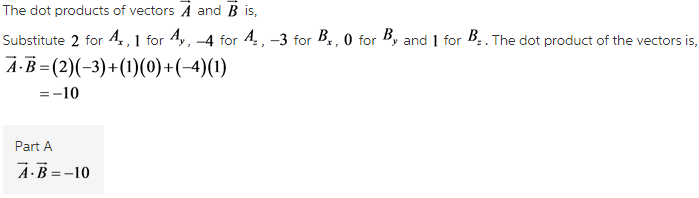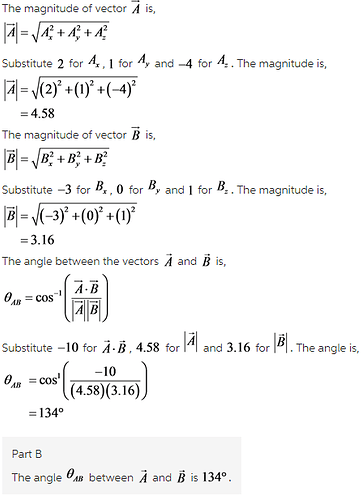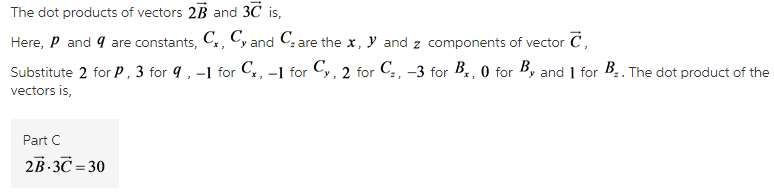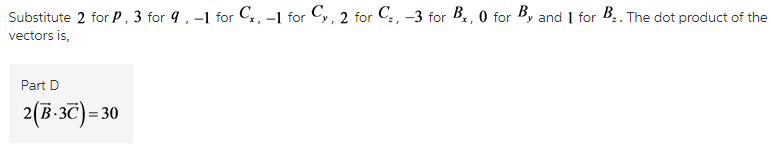Let vectors A⃗ =(2,1,−4), B⃗ =(−3,0,1), and C⃗ =(−1,−1,2).
Calculate the following:
A) A⃗ ⋅B⃗ =
B)What is the angle θAB between A⃗ and B⃗ ?
C) 2B⃗ ⋅3C⃗ =
D)2(B⃗ ⋅3C⃗ ) =
E)Which of the following can be computed?
F) Express your answer in terms of V1: V⃗ 1⋅V⃗ 1 =
G)If V⃗ 1 and V⃗ 2 are perpendicular,
H) If V⃗ 1 and V⃗ 2 are parallel,
Express your answer in terms of V1 and V2.
Concepts and reason
The main concept used to solve the problem is the vector operations.
Initially, use the components of the given vectors to find the magnitude of the vectors. find the dot product of the vector using the components of the vector. Later, use the dot product of the vectors and the magnitude of the vector to find the angle between the vectors. Finally, multiply the vectors with corresponding constants and calculate dot product.
Fundamentals
The multiplication of a vector with a constant can be done by multiplying the component of the vector by the constant.
The dot product of two vectors are a scalar.
Amswer:
(A)
The cross product of two vectors is the sum of product of components of the vectors.
(B)
The angle between two vectors depends on the scalar product of the vectors and the magnitude of the vectors.
( C)
The dot product of the vector should multiply with the constant to give the dot product of the vectors multiplied by constants.
(D)
The dot product,
The constant can be taken out and the dot product of the vector alone can be multiplied with the constants.
(E)
The dot product can only take on two vectors. The dot product gives a scalar value.
In (a) 
, the dot product between first two vector gives a scalar and the third vector cannot be taken further for a dot product with the scalar value. Hence the equation is not computable.
In (b) 
, the dot product between last two vector gives a scalar and the first vector cannot be taken further for a dot product with the scalar value. Hence the equation is not computable.
In ( c) 
, the addition between last two vector gives a vector and the first vector can be taken further for a dot product with the sum of last two vectors. Hence the equation is computable.
In (d) 
, 3 is a scalar, hence the vector 
cannot undergo dot product with the scar. The equation is not computable.
The operation which is computable is ( c) .
Part E
The operation which is computable is ( c) .
(F)
The dot product of single vector with itself is the square of magnitude of the vector.
(G)
The dot product of two vectors when they are perpendicular to each other is zero.
(H)
The dot product of two parallel vectors is the product of magnitudes of them.