In the given figure, m and n are two plane mirrors parallel to each other. Show that the incident ray CA is parallel to the reflected ray BD.
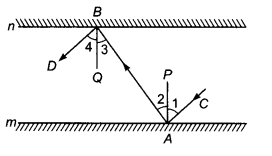
Given, two plane mirrors m and n, such that m || n. An incident ray CA after reflection takes the paths AB and then BD. AP and BQ are the normals to the plane mirrors m and n, respectively.
Since, AP⊥ m, BQ ⊥ n and m || n
∴ AP⊥ n, BQ ⊥m => AP || BQ
Thus, AP and BQ are two parallel lines and a transversal AB cuts them at A and B, respectively.
∴ ∠2 =∠3 …(i)
[alternate interior angles]
But ∠1 = ∠2 …(ii)
and ∠3=∠4 …(iii)
[by the laws of reflection]
∴∠1 + ∠2 = ∠2 + ∠2
[adding ∠2 on both sides of Eq. (ii)]
and ∠3+∠4 = ∠3+∠3
[adding ∠3 on both sides of Eq. (iii)]
=> ∠1 +∠2 = 2(∠2) and ∠3 +∠4 = 2(∠3)
=> ∠1 + ∠2 = ∠3 + ∠4
[∵∠2 = ∠3=>2(∠2) = 2(∠3)]
∴ ∠CAB =∠ABD
Thus, lines CA and BD are intersected by transversal AB such that ∠CAB =∠ABD i.e. alternate interior angles are equal.
Hence, AC||BD