In the given figure, BD=DC and ∠CBD = 40°. Find ∠BAC.
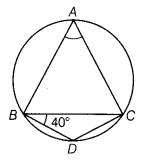
In ∆BDC, BD = DC [given]
∴ ∠DCB =∠CBD = 40…(i)
[∵ angles opposite to equal sides are equal]
Also, ∠CBD +∠BDC + ∠DCB = 180°
[∵sum of angles of a triangle is 180°]
∴ 40° +∠BDC + 40° = 180° [from Eq. (i)]
=> ∠BDC = 180°- 80° = 100°
As A, B, D and C are four points on a circle.
Therefore, ABDC forms a cyclic quadrilateral.
Hence, ∠A +∠D = 180°
[∵ in a cyclic quadrilateral, sum of two opposite angles is equal to two right angles, i.e. 180°]
=> ∠A + 100° = 180° [ ∠D = ∠BDC = 100°]
∴ ∠A = 80°