In the given figure, ABCD is a quadrilateral in which AD = BC, AB||CD and ∠ADC = ∠BCD. Show that the points A,B,C and D lie on a circle.

Given ABCD is a quadrilateral in which AD = BC and ∠ADC = ∠BCD.
To prove ABCD is a cyclic quadrilateral.
Construction Draw DE perpendicular to AB and CF perpendicular to AB.
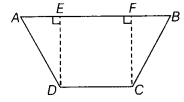
Proof In ∆AED and ∆BFC,
∠ AED = ∠BFC=90° [∵ DE ⊥ AB and CE ⊥ AB]
ED = FC
[ ∵ distance between two parallel lines are equal ]
and AD =BC [given]
![]()
Then, ∠A = ∠B [by CPCT] … ,(i)
and ∠ADE = ∠BCF [by CPCT]
Since, ABCD is a quadrilateral.
∠A+∠B+∠C+∠D=360°
[∵ sum of all angles of a quadrilateral is 360°]
⇒∠B + ∠B + ∠D + ∠D = 360° [from Eq. (i)]
⇒2 ∠B + 2 ∠D=360°
⇒∠B + ∠D=180°
Hence, ABCD is a cyclic quadrilateral because the sum of opposite angles is 180°.