In the calculation of packing efficiency of hcp arrangement,the height of the unit cell is taken as 4r√2/3. Why?
In the hexagonal closest-packed structure, a = b = 2r and c = 4 √2/3 r , where r is the atomic radius of the atom. The sides of the unit cell are perpendicular to the base, thus α = β = 90o
For a closest-packed structure, the atoms at the corners of base of the unit cell are in contact, thus a = b = 2 r. The height © of the unit cell, which is more challenging to calculate, is c = 2a √2/3 r = 4 √2/3 r.
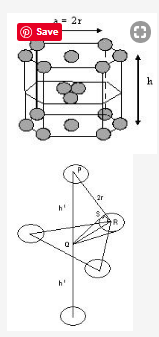
Let the edge of hexagonal base =a
And the height of hexagon = h
And radius of sphere = r
The centre sphere of the first layer lies exactly over the void of 2nd layer B.
The centre sphere and the spheres of 2nd layer B are in touch
So, In Δ PQR (an equilateral triangle)
PR = 2r, Draw QS tangent at points
∴ In Δ QRS ∠QRS = 30°, SR = r
Cos30° = SR/QR
QR = r / √3/2 = 2r / √3
∴ PQ = √PR2 – QR2 = √4r2 – 4r2 / 3
h1 = √8r2 / 3 = 2 √2/3 r
∴ h = 2h1 = 4 √2/3 r
Hence, in the calculation of packing efficiency of hcp arrangement,the height of the unit cell is taken as 4r√2/3.