In the adjoining figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (∆APQ).
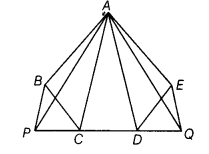
Given ABCDE is a pentagon, in which BP || AC and EQ || AD.
To prove ar (ABCDE) = ar (AAPQ)
Proof We know that triangles on the same base and between the same parallels are equal in area.
∴ ar (∆ADE) = ar (∆ADQ) ,…(i)
[∵∆ADQ and ∆ADE lie on the same base AD and between the same parallels AD and EQ]
Similarly, ar (∆CAB) = ar ∆(CAP) …(ii)
[∵same base is AC and same parallels are AC and BP]
On adding Eqs. (i) and (ii), we get
ar (∆ADE) + ar (∆CAB)
= ar (∆ADQ) + ar (∆CAP) (1)
On adding ar(∆CDA) both sides, we get
ar (∆ADE) + ar (∆CAB) + ar(∆CDA)
= ar (∆ADQ) + ar (∆CAP) + ar(∆CDA)
=> ar (ABCDE) = ar (∆APQ)