In quadrilateral ABDC, AB = AC and AD is the bisector of ∠BAC. Anju has to prove that∆ABD =∆ACD, which as follows
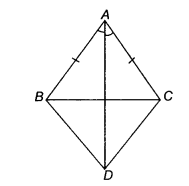
Here, AB = AC [given]
∠BAD = ∠CAD
[∵AD is bisector of ∠BAC]
and ∠B = ∠C [∵corresponding angles of equal sides are equal] .
∆ABD = ∆ACD [by ASA congruence rule]
Further Anju shows this proof to his classmate Amita and she finds that there is some errors in the proof.
(i) Write the correct proof.
(ii) What is the mistake in Anju’s proof?
(iii) Which value is depicted from this action?


(ii) Anju has used the result ∠B =∠C for proving ∆ABD = ∆ACD, but it is possible only when we consider ∆ABC.
(iii) The value depicted from this action, is cooperative learning among students without any bias.