In ∆PQR, the sides PQ, PR are equal and the base QR is produced to any point M. From M, MO is drawn perpendicular to PQ produced and MN perpendicular to PR produced. Prove that QM bisects∠OMN.
Given In ∆PQR, PQ = PR and the base QR is produced to M.
From M, MO is drawn perpendicular to PQ produced at O and MN is perpendicular to PR produced at N.
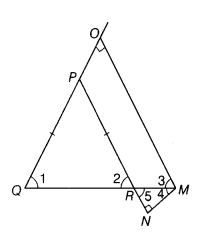
To prove QM bisects ∠OMN.
Proof In ∆PQR,
PR = PQ [given]
⇒ ∠2 = ∠1 …(i)
[∵ angles opposite to equal sides are equal.]
In right angled ∆QOM, we have
∠1 + ∠3 + ∠QOM = 180°
[by angle sum property of a triangle]
⇒ ∠1+∠3 + 90° = 180°
[∵OM⊥QO ⇒∠QOM = 90°]
⇒ ∠1+∠3 = 90°
⇒ ∠3 = 90°-∠1 …(ii)
In right angled ∆RNM, we have
∠4+ ∠5+ ∠RNM = 180°
[by angle sum property of a triangle]
⇒∠4+ ∠5+ 90°= 180°
[∵MN⊥PN;⇒ ∠RNM = 90°]
⇒ ∠4+ ∠5 = 90°
⇒ ∠4= 90°-∠5
⇒ ∠4 = 90°-∠2 …(iii)
[∵ ∠2 =,∠5, vertically opposite angles]
From Eqs. (i), (ii) and (iii), we get
∠3 = ∠4
Hence, QM bisects∠OMN.