In figure, ABCD is a trapezium in which side AB is parallel to DC and E is the midpoint of side AD. If F is a point of side BC such that the segment EF||DC, prove that EF= 1/2(AB+DC)
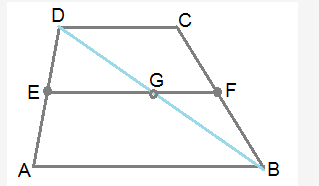
Figure shows the trapezium ABCD.
AB || CD (given)
E is mid point of AD (given)
EF || DC (given)
Let us join BD and let EF meets BD at G.
since EF || DC and AB || DC, we have EG || AB.
In Δ ABD, EG || AB and E is mid point of AD. Hence EG = (1/2)AB and BG = DG …(1)
similarly we can say GF || DC.
in Δ BCD, FG || CD and G is mid point of BD. Hence GF = (1/2)DC …(2)
from (1) and (2), we have EG+GF = EF = (1/2)(AB+DC)