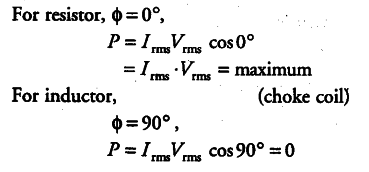Answer the following questions:
(i) In any AC circuit, is the applied instantaneous voltage equal to the algebraic sum of instantaneous voltage across the series elements of the circuit? Is the same true for rms voltage?
(ii) A capacitor is used in the primary circuit of an induction coil. Why?
(iii) An applied voltage signal consists of superposition of a DC voltage and an AC voltage of high frequency. The circuit consists of am inductor and a capacitor in series. Show that the DC signal will appear across C and the AC signal across L.
(iv) A choke coil in series with a lamp is
connected to a DC line. The lamp is seen to shine brightly. Insertion of an iron core in the choke causes no change in the lamp’s brightness. Predict the corresponding
observations, if the connection is to an AC line.
(v) Why is choke coil needed in the use of
fluorescent tubes with AC mains? Why we cannot use an ordinary resistor instead of the choke coil?
(i) Yes, it is true for instantaneous voltage.
No, it is not true for rms voltaige because voltages across various elements may not be in same phase.
(ii) Because when the circuit is broken, then the large
amount of induced voltage is used up in charging the capacitor. Thus, sparking is avoided.
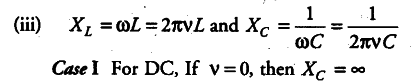
Thus, capacitor blocks DC
Case II For AC of higher frequency, thus the inductor blocks the current. Hence, AC signal appears across L.
(iv)
A choke has no impedance, if it is connected to DC line. Therefore, lamp shines brighdy and has no effect on inserting iron core in the choke. But choke offers impedance, if it is connected to AC line. So the bulb lights dimly. When an iron core is inserted in the choke, the impedance to AC. increases. Hence, the brightness of the bulb decreases.
(v) We use the choke coil instead of resistance because the power loss across resistor is maximum, while the power loss across choke is zero.