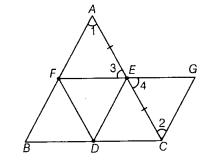
In ∆ABC; D, E and F are mid-points of sides BC,AC and AB, respectively. A line through C drawn parallel to DE meets FE produced to G. Show that ar (∆FDE) = ar (∆EGC)
∵D and F are the mid-points of BC and AB respectively. Using mid-point theorem in ∆ABC
![]()
i.e. FD = AE and FD||AE i.e. AFDE is a parallelogram.
∴ ar (∆FAC) = ar (∆FDE) ,…(i)
[∵ FE diagonal of ||Parallelogram which divides two equal triangles]
In ∆FAE and ∆GCE,
∠1 = ∠2 [alternate interior angles]
AE = EC [given]
∠3 = ∠4 [vertically opposite angles]
∴ ∆FAE =∆GCE [by ASA Congruence rule]
So, ar (∆FAE) = ar (∆GCE)
i. e. ar(∆FAE)=ar(∆EGC) …(ii)
from Eqs. (i) and (ii), we have
ar (∆FDE) = ar (∆EGC)