In a quadrilateral ABCD, there is a point O inside it such that OB = OD

CBSE Class 9 CBSE Class 9 Maths
1

In a quadrilateral ABCD, there is a point O inside it such that OB = OD. Also, AB = AD and BC = DC. Prove that O lies on AC

2

In ∆AOB and ∆AOD,
AB = AD
OB=OD
OA=OA
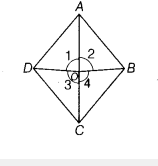
image
∠1 = ∠2
image
Similarly, in ∆CBO and ∆CDO,
BC = DC [given]
OB = OD [given]
and OC = OC [common side]

image
∠3 = ∠4
On adding Eqs. (i) and (ii), we get ∠1+∠3 = ∠2 +∠4

We know that∠1 +∠3+∠2 +∠4 = 360

[∴ sum of all angles around a point is 360°]
∠1 + ∠3+ ∠1 + ∠3 = 360° [from Eqs. (I) and (ii)]
2(∠1+∠3) = 360°
∠1+∠3 = 180°
∠AOC = 180°

Hence, O lies on AC.