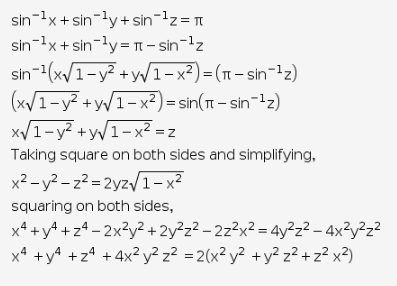If sin^-1x+sin^-1y+sin^-1z=pi,prove that

CBSE Class 12
1

If sin-1x+sin-1y+sin-1z=pi,prove that

(i) x(1-x2)1/2 +y(1-y2)1/2 +z(1-z2)1/2=2xyz
(ii) x4 +y4 +z4 +4x2 y2z2 =2(x2 y2 +y2 z2+z2– x2

2

image
image