how to solve root 10 and 7.3 on number line
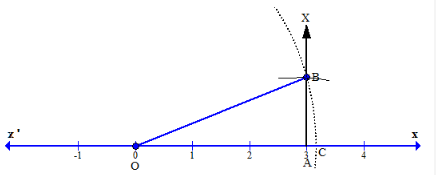
Consider a number line. Let the point O represent 0 and point A represent 3.
Now draw a perpendicular AP at A on the number line and cut off arc AB = 1 unit.
Using Pythagoras Theorem, we have
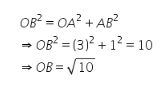
With O as the centre and
as radius draw an arc cutting real line at C. Clearly,
Thus, C represents 
on the number line.
Now let us find the square root of 7.3
Make a list of perfect squares, 0, 4, 9, 16, 25, 36, …
Identify perfect squares closest to 7.3
Thus we have, 4 < 7.3 < 9
Take a positive square root of each number.
Thus, we have
Now evaluate the square roots.
Therefore, we have,
Now make a list of perfect squares between 2 and 3.
| Numbers | Squares |
|---|---|
| 2.1 | 4.41 |
| 2.2 | 4.84 |
| 2.3 | 5.29 |
| 2.4 | 5.76 |
| 2.5 | 6.25 |
| 2.6 | 6.76 |
| 2.7 | 7.29 |
| 2.8 | 7.84 |
| 2.9 | 8.41 |
Thus, from the list it is clear that, 7.29 is closer to 7.3.
Therefore, we have,
Thus, we can mark 2.7 on the number line as follows:
Thus, OA represents the square root of 7.3