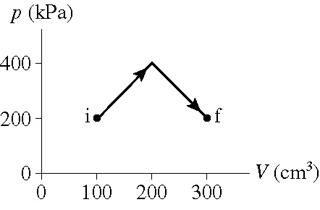
How much work is done on the gas in the process shown in the figure ?
Concepts and reason
The concept used to solve this problem is work done.
First, by splitting the space under the curve into a rectangle and a triangle, find the area of the rectangular space. Then find the area of the triangular space. Finally, combine the areas to find the area under the curve and calculate the work done.
Fundamentals
Gasses can do work by either expansion or compression against an external pressure. This work done is called pressure-volume work. This work done is given by the expression,

Thus, the work done will be negative if the gas is expanding because the change in volume will be positive. Similarly, the work done is positive if the gas is compressed because the change in volume will be negative.
The area of a rectangle is given by the equation
![]()
Here, a is the length of the rectangle and b is the breadth of the rectangle.
The area of a triangle is,
![]()
Here,b is the base length of a triangle and h is the height of the triangle from the base.
Answer:
Find the area of the rectangular space.
The area of a rectangle is,
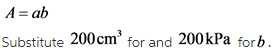

Explanation:
The space under the graph shown can be split into two shapes, a rectangular space and a triangular space. The total area under the graph will give the work done on the graph. As the x axis of the graph is volume and the y axis of the graph is pressure, by finding the area of the rectangle, we will get the work done.
The area of the rectangular part is
A = ab
Where, a is the length of the rectangle and b is the breadth of the rectangle.
Find the area of the triangular space.
The area of a triangle is,
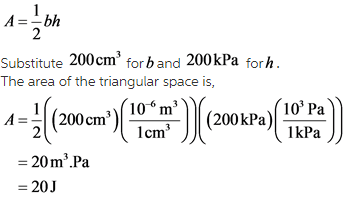
Explanation:
Combining the area of the rectangular space and the triangular space, the work done on the gas can be found. The area of the triangular space is,
![]()
As b is volume and h is pressure, the product will be work done and the unit is Joules.
Find the work done on the gas.
The total work done is the area under the given curve, which is the sum of the area of the rectangular space and the triangular space.
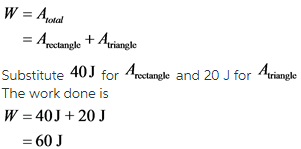
The work done in expanding a gas is negative. In the graph shown, the volume of the gas is increasing. So, the gas is expanding and the work done is negative. Thus,
![]()

Explanation:
The work done in a graph with pressure in the y axis and volume in the x axis is the area under the graph. The area under the graph show is the sum of the area of the rectangle and the area of the triangle.
![]()
The work done against the external pressure by a gas when it expends or compress is,
![]()
For an expanding gas, the change in volume is positive. So, the work done is negative.